一、率的标准误
用十抽十样方法进行研究时,必然存在十抽十样误差。率的十抽十样误差大小可用率的标准误来表示,计算公式如下:
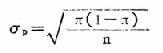
公式(20.5)
式中:σp为率的标准误,π为总体十陽十性十率,n为样本含量。因为实际工作中很难知道总体十陽十性十率π,故一般采用样本率p 来代替,而上式就变为
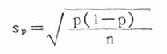
公式(20.6)
例 20.5河北省组织高碘地方十性十甲状腺肿流行病学调查,作者调查了饮用不同碘浓度井水居民甲状腺肿的患病情况,其中有两组资料如下表,试分别求出率的标准误。
水中含碘量均数(μg/L) 受检人数 患病人数 患病率(%) 458.25 3315 59 1.78 825.95 3215 180 5.60
计算法:第一组:n1=3315,p1=1.78%=0.0178
1-p1=1-0.0178=0.9822

第二组:n2=3215,p2=5.60%=0.056
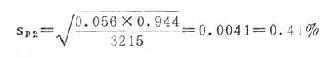
1-p2=1-0.056=0.944
二、总体率的可信区间
由于样本率与总体率之间存在着十抽十样误差,所以也需根据样本率来推算总体率所在的范围,根据样本含量n和样本率P的大小不同,分别采用下列两种方法:
(一)正态近似法
当样本含量n足够大,且样本率P和(1-p)均不太小,如np或n(1-p)均≥5时,样本率的分布近似正态分布,则总体率的可信区间可由下列公式估计:
总体率(π)的95%可信区间:p±1.96sp
总体率(π)的99%可信区间:p±2.58sp
例如前述两组高碘地方十性十甲状腺肿患病率的总体患病率可信区间为:
第一组:
95%可信区间为1.78%±1.96×0.23%=1.33%~2.23%
95%可信区间为1.78%±2.58×0.23%=1.19%~2.37%
第二组:
95%可信区间为5.6%±1.96×0.41%=4.80%~6.40%
95%可信区间为5.6%±2.58×0.41%=4.54%~6.66%
(二)查表法
当样本含量n较小,如n≤50,特别是p接近0或1时,则按二项分布原理确定总体率的可信区间,其计算较繁,读者可根据样本含量n和十陽十性十数X参照专用统计学介绍的二项分布中95%可信限表。

