第一节 集中趋势指标
平均数是统计中应用最广泛、最重要的一个指标体系。常用的有算术均数、几何均数、中位数三个指标。它们用于描述一组同质计量资料的集中趋势或反映一组观察值的平均水平。
一、算术均数(arithmetic mean)
简称对数(mean)。十习十惯上以表示样本均数,以希腊字母μ表示总体均数。均数适用于对称分布,特别是正态或近似正态分布的计量资料,其计算方法有:
(一)直接法
当样本的观察值个数不多时,将各观察值X1,X2,……,Xn相加再除以观察值的个数n(样本含量)即得均数。其公式为:
 公式(18.1)
公式(18.1)
式中,希腊字母Σ(读作sigma)是求和的符号。
例18.1 某地11名20岁健康男大学生身高(cm)分别为174.9,173.1, 171.8,179.0,173.9,172.7,166.2,170.8,171.8,172.1,168.5。试计算其均数。

(二)加权法
当观察值个数较多时,可先将各观察值分组归纳成频数表,用加权法求均数。其计算步骤如例18.2。
例18.2 某地1993年随机测量了该地110名20岁健康男大学生的身高(cm),资料如下,试计算其均数。
| 173.9 | 173.9 | 166.9 | 179.5 | 171.2 | 167.8 | 177.1 | 174.7 | 173.8 | 182.5 |
| 173.6 | 165.8 | 168.7 | 173.6 | 173.7 | 177.8 | 180.3 | 173.1 | 173.0 | 172.6 |
| 173.6 | 175.3 | 178.4 | 181.5 | 170.5 | 176.4 | 170.8 | 171.8 | 180.7 | 170.7 |
| 173.8 | 164.4 | 170.0 | 175.0 | 177.7 | 171.4 | 162.9 | 179.0 | 174.9 | 178.3 |
| 174.5 | 174.3 | 170.4 | 173.2 | 174.5 | 173.7 | 173.4 | 173.9 | 172.9 | 177.9 |
| 168.3 | 175.0 | 172.1 | 166.9 | 172.7 | 172.2 | 168.0 | 172.7 | 172.3 | 175.2 |
| 171.9 | 168.6 | 167.6 | 169.1 | 166.8 | 172.0 | 168.4 | 166.2 | 172.8 | 166.1 |
| 173.5 | 168.6 | 172.4 | 175.7 | 178.8 | 169.1 | 175.5 | 170.3 | 171.7 | 164.6 |
| 171.2 | 169.1 | 170.7 | 173.6 | 167.2 | 170.7 | 174.7 | 171.8 | 167.3 | 174.8 |
| 168.5 | 178.7 | 177.3 | 165.9 | 174.0 | 170.2 | 169.5 | 172.1 | 178.2 | 170.9 |
| 171.3 | 176.1 | 169.7 | 177.9 | 171.1 | 179.3 | 183.5 | 168.5 | 175.5 | 175.9 |
1.编制频数表
(1)求全距(range):找出观察值中的最大值(183.5)和最小值(162.9),它们的差值即全距,常用R表示。本例R=20.6。
(2)定组距和组段:相邻两组的最小值之差称组距,常用i表示,各组距可相等,也可不相等,一般用等距。常取全距的1/10,取整作组距。本例全距的1/10为2.06,取整为2,用等距共划分11个组段。第一组段应包括资料中最小值,最末组段应包括最大值,一般要求组段的起点为较整齐的数。本例第一组段的起点(即下限)取162,其止点(即上限)为第二组段的起点即164,然后每一组距(本例为2)就成为一组段,最末组段应同时写出下限和上限,本例为182~184。
(3)列表划记:按上述的组段序列排列制表,用正字划记法将例18.2中的数据归纳到各组段中,最后清点出频数得频数表,表18-1中的第(2)、(3)栏。
表18-1 110名20岁健康男大学生身高(cm)的频数分布
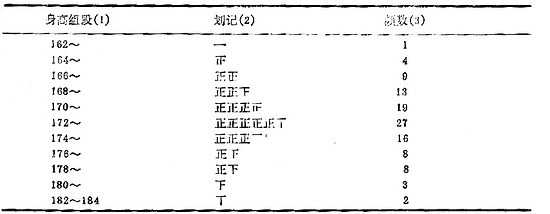
由频数表的频数分布可看出两个重要特征:集中趋势和离散趋势。集中趋势即频数分布向中央部分集中;离散趋势即频数分布由中央到两侧逐渐减少。频数分布可为①对称分布或近似正态分布,即集中位置在正中,两侧频数分布大致对称,如表18-1;②偏态分布,即集中位置偏向一侧,频数分布不对称,若集中位置偏向数值小的一侧,为正偏态分布;若集中位置偏向数值大的一侧,为负偏态分布。不同类型的分布,应采用相应描述指标和统计分析方法。
2.计算公式
 公式(18.2)
公式(18.2)
式中,k为组段数;f1,f2,……,fk分别为各组段的频数;X1,X2,……,Xk分别为各组段的组中值,组中值为本组段的下限与相邻较大组段的下限相加除以2,如“162-”组段的组中值X1=(162+164)/2=163,余仿此。
3.列计算表(表18-2)计算均数

110名20岁健康男大学生身主的均数为172.73(cm)。
二、几何均数(geometric mean)
用G表示。常用于等比级数资料和对数对称分布,尤其是对数正态分布的计量资料。对数正态分布即原始数据呈偏态分布,经对数变换后(用原始数据的对数值lgX代替X)服从正态分布。其计算方法有:
表18-2 110名20岁健康男大学生身高(cm)均数的计算表(加权法)
| 身高级段(1) | 组中值X(2) | 频数f(3) | FX(4)=(2)×(3) |
| 162~ | 163 | 1 | 163 |
| 164~ | 165 | 4 | 660 |
| 166~ | 167 | 9 | 1503 |
| 168~ | 169 | 13 | 2197 |
| 170~ | 171 | 19 | 3249 |
| 172~ | 173 | 27 | 4671 |
| 174~ | 175 | 16 | 2800 |
| 176~ | 177 | 8 | 1416 |
| 178~ | 179 | 8 | 1432 |
| 180~ | 181 | 3 | 543 |
| 182~184 | 183 | 2 | 366 |
| 合计 | 110(Σf) | 19000(ΣfX) |
(一)直接法
当观察值个数n不多时,直接将n个观察值(X1,X2,……Xn)的乘积开n次方。其计算公式为:
 公式(18.3)
公式(18.3)
其对数形式:
 公式(18.4)
公式(18.4)
例18.3 设有6份血清的抗体效价为1:10,1:20,1:40,1:80,1:80,1:160。求其平均效价。
本例可将各抗体效价的倒数代入公式(18.4),求平均效价数的倒数。

该6份血清的平均抗体效价为1:45。
(二)加权法
当观察值个数n较多时,先将观察值分组归纳成频数表,再用公式(18.5)计算。
 公式(18.5)
公式(18.5)
式中,X为各组段的效价或滴度的倒数(等比级数资料时)或各组段的组中值(对数正态分布资料时);f 为各组段所对应频数。
例18.430名麻疹易感儿童接种麻疹疫苗一个月后,血凝抑制抗体滴度如表18-3第(1)、(2)栏,试求其平均抗体滴度。

30名麻疹易感儿童免疫后的平均血凝抑制滴度为1:48.5。
三、中位数(median)
中位数是一组按大小顺序排列的观察值中位次居中的数值,用M表示。它常用于描述偏态分布资料的集中趋势。中位数不受个别特小或特大观察值的影响,特别是分布末端无确定数据不能求均数和几何均数,但可求中位数。计算方法有:
表18-3 平均抗体滴度计算表
| 抗体滴度(1) | 人数f(2) | 滴度倒数X(3) | lgX(4) | flgX(5)=(2)×(4) |
| 1:8 | 2 | 8 | 0.9031 | 1.8062 |
| 1:16 | 6 | 16 | 1.2041 | 7.2246 |
| 1:32 | 5 | 32 | 1.5051 | 7.5255 |
| 1:64 | 10 | 64 | 1.8062 | 18.0620 |
| 1:128 | 4 | 128 | 2.1072 | 8.4288 |
| 1:256 | 2 | 256 | 2.4082 | 4.8164 |
| 1:512 | 1 | 512 | 2.7093 | 2.7093 |
| 合计 | 30(Σf) | 50.5728(ΣflgX) | ||
(一)直接法
当n较小时,可直接由原始数据求中位数。先将观察值由小到大按顺序排列,再按公式(18.6)或公式(18.7)计算。
 公式(18.6)
公式(18.6)
(n为偶数时) 公式(18.7)
式中,n 为观察值的总个数,X的右下标(n+1/2)、(n/2)、和(n/2+1)为有序数列中观察值的位次,X(n+1/2)、X(n/2)和X(n/2+1)为相应位次上的观察值。
例18.5 某病患者9名,其发病的潜伏期顺序为2,3,3,3,4,5,6,9,16天,求中位数。
本例n=9,为奇数,按公式(18.6)计算

若上例在第20天又发现一例患者,则患者数增为10名,n为偶数,按公式(18.7)计算

(二)频数表法
当n较大时,先将观察值分组归纳成频数表,再按组段由小到大计算累计频数和累计频率。如表18-4中的(3)、(4)两栏,然后按公式(18.8)计算。
 公式(18.8)
公式(18.8)
式中,L为中位数(即累计频率为50%)所在组段的下限;i为该组段的组距;f为该组段的频数;ΣfL为小于L的各组段的累计频数;n为总例数。
例18.6 求表18-4中数据的中位数
表18-4 164名食物中毒潜伏期的中位数和百分位数*计算表
| 潜伏期(小时 )(1) | 人数f(2) | 累计频数(Σf)(3) | 累计频率(%)(4) |
| 0~ | 25 | 25 | 15.2 |
| 12~ | 58 | 83 | 50.6 |
| 24~ | 40 | 123 | 75.0 |
| 36~ | 23 | 146 | 89.0 |
| 48~ | 12 | 158 | 96.3 |
| 60~ | 5 | 163 | 99.4 |
| 72~84 | 1 | 164 | 100.0 |
*百分位数的意义与计算见后面的[附].
由表18-4可见,50%在“12~”组段内,则L=12,i=12,f=58,ΣfL=25,n=164,按式(18.8)计算
M=L+i/f(n/2-ΣfL)=12+12/58(164/2-25)=23.8(小时)
[附]百分位数:百分位数是一个位置指标,用Px表示。当P1,P2,……,P98,P99确定后,一个由小到大的有序数列即被分为100等份,各含1%的观察值。百分位数常用于描述一组偏态分布资料在某百分位置上的水平及确定偏态分布资料的医学正常值范围。第50百分位数(P50)也就是中位数,所以,中位数也是一个特定的百分位数。计算百分位数用公式(18.9)
Px=L+i/fx(n.x%-ΣfL)公式(18.9)
式中,L、i、fx分别为Px所在组段的下限、组距和频数;ΣfL为小于L的各级段的累计频数。
例18.7 求表18-4中数据的P95。
求P95时,x=95,即累计频率为95%所在组段。本例为“48~”组段,则L=48,i=12,fx=12,ΣfL=146,n=164,代入公式、(18.9)
P95=48+12/12(164×95%-146)=57.8(小时)
第二节 离散趋势指标
计量资料的频数分布有集中趋势和离散趋势两个主要特征,只有把两者结合起来,才能全面地认识事物,通过例18.8可进一步说明这一问题。
例18.8 有3组同龄男孩体重(kg)如下,其平均体重x都是30(kg),试分析其离散趋势。
| 甲组 | 26 | 28 | 30 | 32 | 34 |
| 乙组 | 24 | 27 | 30 | 33 | 36 |
| 丙组 | 26 | 29 | 30 | 31 | 34 |
虽然三组资料的均数相等,即集中趋势相同,但各组内数据参差不齐的程度(变异度)不同,也就是说三组的离散趋势不同。
描述一组同质计量资料离散趋势的常用指标有全、四分位数间距方差和标准差,其中方差和标准差最常用。
一、全距(range)
亦称极差,用R表示。全距是一组观察值中最大值与最小值之差,用于反映个体变异范围的大小。全距大,说明变异度大;反之,说明变异度小。如例18.8中乙组全距为12(kg),比甲、丙两组8(kg)大,表明乙组变异度大。全距适用于任何分布的计量资料(末端无确切数值者除外)。
用全距来表达变异度的大小,简单明了,故曾广为使用。但它不能反映组内所有数据的变异度,如上述甲、丙两组变异度的差异就反映不出来;其更大的缺点是易受个别特大或特小数值的影响,往往样本越大,全距亦会越大。
二、四分位数间距(quartile interval)
四分位数间距是上四分位数Qu(即P75)与下四位数QL(即P25)之差,其间包括了全部观察值的一半,用Q表示。它和极差类似,数值越大,说明变异越大;反之,说明变异越小。四分位数间距比极差稳定,但仍未考虑到每个观察值的变异度。它适用于偏态分布资料,特别是分布末端无确定数据不能计算全距、方差和标准差的资料。
例18.9 求表18-4中数据的四分位数间距。
QL=P25=12+12/58(164×25%-25)=15.3(小时)
Qu=P75=24+12/40(164×75%-83)=36.0(小时)
Q=Qu-QL=P75-P25=20.7(小时)
三、方差(variance)和标准差(standard deviation)
为了克服极差的缺点,需全面地考虑组内每个观察值的离散情况。因为组内每一观察值(亦称变量值)与总体均数的距离大小都会影响总体的变异度,故有人提出以各变量值离均差(X-μ)的平方和除以变量值的总个数N,来反映变异度大小,称为总体方差,用σ2示之。
 公式(18.10)
公式(18.10)
由式可见,各个离均差平方后,原来的度量单位变成了平方单位。为了用原单位表示而将总体方差开方,称为总体标准差。
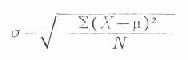 公式(18.11)
公式(18.11)
以上是总体方差和标准差。实际工作中经常得到的是样本资料,μ是未知的,只能用样本均数x来代替μ,用样本含量n代替N,按公式(18.11)算得的标准差常比σ小,美国统计学家W.S.Gosset提出用n-1代替n,求得样本标准差s,即
 公式(18.12)
公式(18.12)
式中的n-1,在统计学上称为自十由度(degree of freedom)
数学上可以证明离均差平方和Σ(X-x)2=ΣX2-(ΣX)2/n,故公式(18.2)可演变为:
直接法 公式(18.13)
公式(18.13)
加权法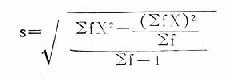 公式(18.14)
公式(18.14)
方差与标准差适用于对称分布,特别是正态或近似正态分布资料。
例18.10 试分别计算例18.8中三组男孩体重资料的标准差。
甲组:n=5,ΣX=26=28+30+32+34=150
ΣX2=262+282+302+322+342=4540
按式(18.13)

乙组:n=5,ΣX=150,ΣX2=4590

丙组:n=5,ΣX=150,ΣX2=4534

以上计算表明:S丙<S甲<S乙亦即乙组的变量度最大,甲组次之,丙组最小。
例18.11 求表18-2中110名20岁健康男大学生身高的标准差。
由表18-2,已知Σf=110,ΣfX=19000,再用第(2)栏乘第(4)栏后相加得ΣfX2。如本例,ΣfX2=163×163+165×660+……+183×366=3283646代入式(18.14)

四、标准差的应用
(一)表示观察值的变异程度(或离散程度)
1.在两组(或几组)资料均数相近、度量单位相同的条件下,标准差大,表示观察值的变异度大,即各观察值离均数较远,均数的代表十性十较差;反之,表示各观察值多集中在均数周围,均数的代表十性十较好。
2.若比较度量单位不同或均数相差悬殊的两组(或几组)观察值的变异度时,需计算变异系数(coefficient ofvariation用CV表示)进行比较,其计算公式为:
CV= s/x×100% 公式(18.15) 公式(18.15)
式中s为样本标准差,x为样本均数。
例18.12 某地调查20岁男大学生110名,其身高均数为172.73(cm),标准差为4.09(cm);其体重均数为55.04(kg),标准差为4.10(kg),欲比较两者变异度何者为大,宜先计算变异系数再比较。
身高CV=4.09/172.73×100%=2.37%
体重CV=4.10/55.04×100%=7.45%
由此可见,该地20名男大学生体重的变异度大于身高的变异度,说明身高这个指标比较稳定。
(二)结合均数描述正态分布的特征和估计医学正常值范围,详见第三节。
(三)结合样本含量n计算标准误,详见第十九章。

